Zhenyu Liang, Hao Li, Naiwei Yu, Kebin Sun and Ran Cheng, Senior Member, IEEE
Abstract
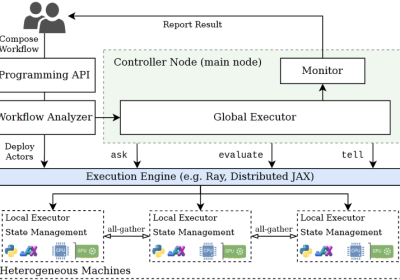
As the demand for sophisticated optimization solutions escalates in fields such as engineering design and energy management, Evolutionary Multiobjective Optimization (EMO) algorithms have gained prominence for their ability to address multiobjective problems effectively. However, traditional CPU-based EMO algorithms encounter significant efficiency bottlenecks when confronted with increasingly large and complex optimization tasks. To overcome this limitation, the EvoX team proposes a unified tensorized representation method for EMO algorithms, harnessing GPU acceleration to enhance performance. Building on this approach, the team has designed and implemented several GPU-accelerated EMO algorithms. Additionally, they have developed “MoRobtrol,” a multiobjective robot control benchmark suite based on the Brax physics engine, to evaluate the efficacy of these algorithms. Leveraging these advancements, the EvoX team has created EvoMO, a GPU-accelerated EMO algorithm library that supports efficient modeling and tackles large-scale optimization challenges. The source code is openly accessible on GitHub: https://github.com/EMl-Group/evomo.
GPU-Accelerated Tensorization Methodology
In the domain of computational optimization, a tensor refers to a multidimensional array capable of representing scalars, vectors, matrices, and higher-dimensional data structures. Tensorization—the process of transforming algorithmic data structures and operations into tensor forms—enables algorithms to capitalize on the parallel computing capabilities of GPUs.
Within EMO algorithms, key data structures are amenable to tensorized representation. For instance, the population of individuals can be expressed as a solution tensor X, where each row vector corresponds to an individual, while the objective function values form an objective tensor F. Auxiliary structures, such as reference vectors or weight vectors, are similarly represented as tensors R or W. This unified tensor framework allows the algorithm to process the entire population collectively at the representation level, establishing a foundation for large-scale parallel computation.
The tensorization of EMO operations, a critical step for boosting computational efficiency, operates on two levels: basic tensor operations and control flow tensorization. Basic tensor operations constitute the core of tensorized EMO implementations (detailed in Table 1), encompassing fundamental computations such as selection, crossover, and mutation in tensor form. Control flow tensorization, meanwhile, replaces conventional iterative and conditional logic with tensor-based equivalents. For example, for / while loops are transformed into batch operations using broadcasting or higher-order functions like vmap, while if-else statements are managed through masking techniques, encoding logical conditions as boolean tensors to alternate between computational paths.

Compared to traditional EMO implementations, tensorization offers several advantages:
- Flexibility: It adeptly handles multidimensional data, surpassing the limitations of traditional two-dimensional matrix operations.
- Efficiency: By leveraging parallel computing, it eliminates the overhead of explicit loops and conditional branching, markedly enhancing performance.
- Simplified Code Structure: It produces more concise and maintainable code, improving readability and ease of upkeep.
As illustrated in Figure 1, the detection of Pareto dominance relationships exemplifies these benefits. Traditional methods rely on nested loops for pairwise comparisons, whereas the tensorized approach employs broadcasting and masking for parallel execution, reducing code complexity and runtime.

Tensorization aligns seamlessly with GPU acceleration due to the GPU’s extensive parallel cores and single-instruction multiple-thread architecture, which are particularly suited to tensor computations, especially matrix operations. Specialized hardware, such as NVIDIA’s Tensor Cores, further amplifies the throughput of tensor operations. Algorithms exhibiting high parallelism, independent computational tasks, and minimal conditional branching are ideal candidates for tensorization. Even for algorithms like MOEA/D, which feature sequential dependencies, effective parallel acceleration is achievable through structural refactoring and the decoupling of key computations.
Application Examples of Algorithm Tensorization
The EvoX team has applied the tensorization methodology to three classic EMO algorithms: NSGA-III (dominance-based), MOEA/D (decomposition-based), and HypE (indicator-based). This section elaborates on MOEA/D as a representative case, with details on NSGA-III and HypE available in the full paper.
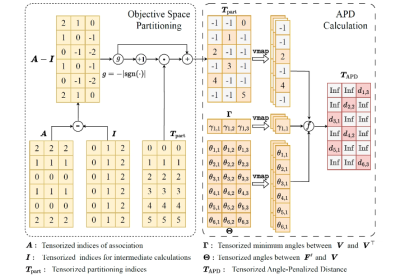
Traditionally, MOEA/D decomposes a multiobjective problem into multiple subproblems, optimizing each independently (see Figure 2). The algorithm comprises four core steps—crossover and mutation, fitness evaluation, ideal point update, and neighborhood update—executed sequentially for each individual within a single loop. This sequential processing incurs significant computational overhead for large populations, as each individual must complete all steps in turn, hindering GPU utilization. The neighborhood update, reliant on inter-individual information exchange, further complicates parallelization.

To address these challenges, the EvoX team introduced tensorized expressions within the environmental selection’s inner loop, decoupling the four core steps into independent operations. This enables parallel processing of all individuals, yielding a tensorized MOEA/D algorithm (TensorMOEA/D). Environmental selection is restructured into two primary steps—comparison and population update, and elite solution selection—both implemented via two vmap operations for tensorization (see Figure 3, not provided, for the framework and data flow).
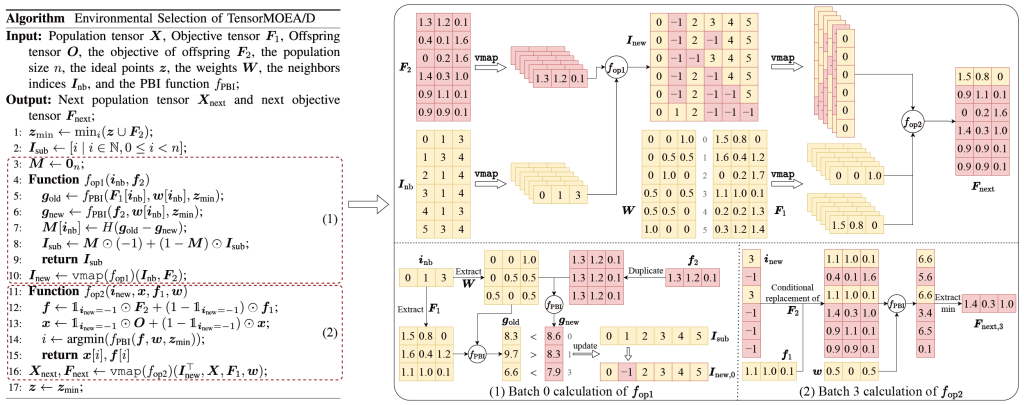
The value of tensorization in EMO algorithms can be summarized in three key aspects:
- Direct Translation from Formulas to Code: Tensorization bridges the gap between mathematical formulations and efficient implementations. For instance, Figure 4 (not provided) demonstrates the seamless conversion of tensorized non-dominated sorting from pseudocode to Python code.
- Simplified Code Structure: Population-level operations are consolidated into unified tensor expressions, minimizing loops and conditionals, thereby enhancing readability and maintainability.
- Enhanced Reproducibility: The structured tensor representation facilitates comparative testing and result replication.

Performance Demonstration
To rigorously evaluate the performance of GPU-accelerated EMO algorithms, the EvoX team conducted three distinct experiments: computational acceleration performance, performance on numerical optimization problems, and optimization effectiveness in multiobjective robot control tasks.
Computational Acceleration Performance
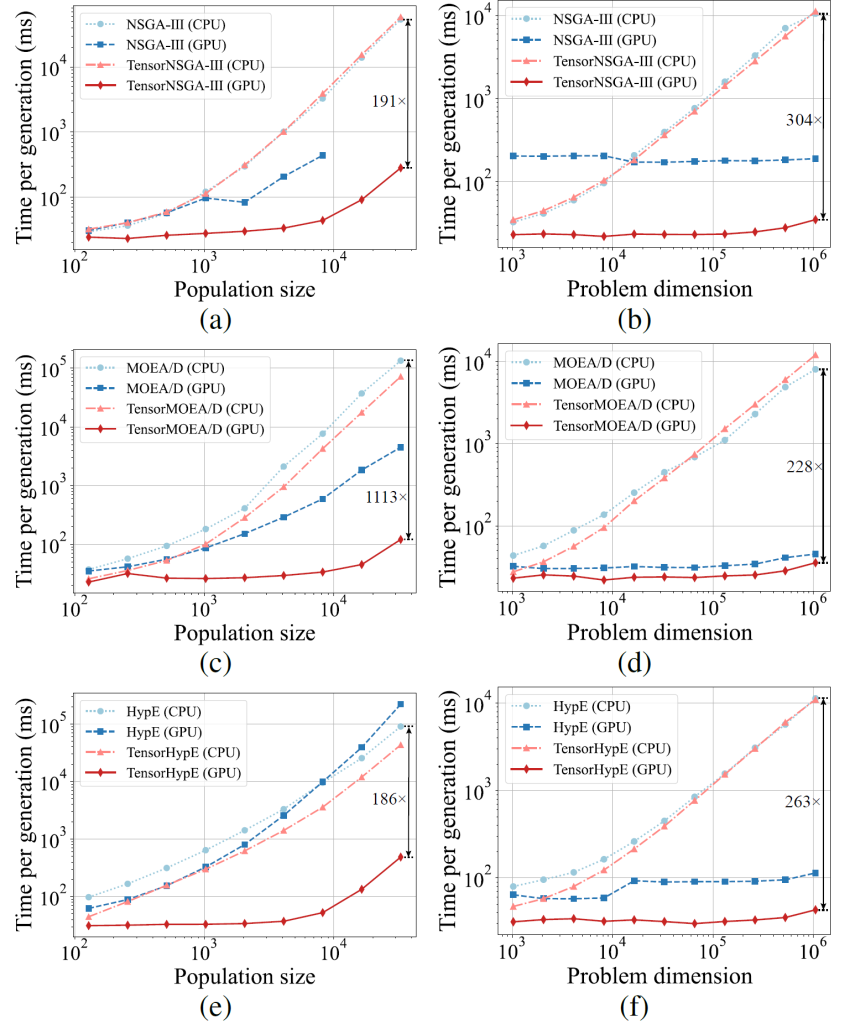
Results in Figure 5, reveal that TensorNSGA-III, TensorMOEA/D, and TensorHypE achieve dramatically faster execution on GPUs compared to their non-tensorized CPU counterparts, with speedups reaching up to 1113 times as scale increases. Tensorized algorithms exhibit robust scalability and stability, with running times growing slowly and maintaining high efficiency, underscoring the transformative impact of tensorization on GPU acceleration.
Performance on LSMOP Test Suite
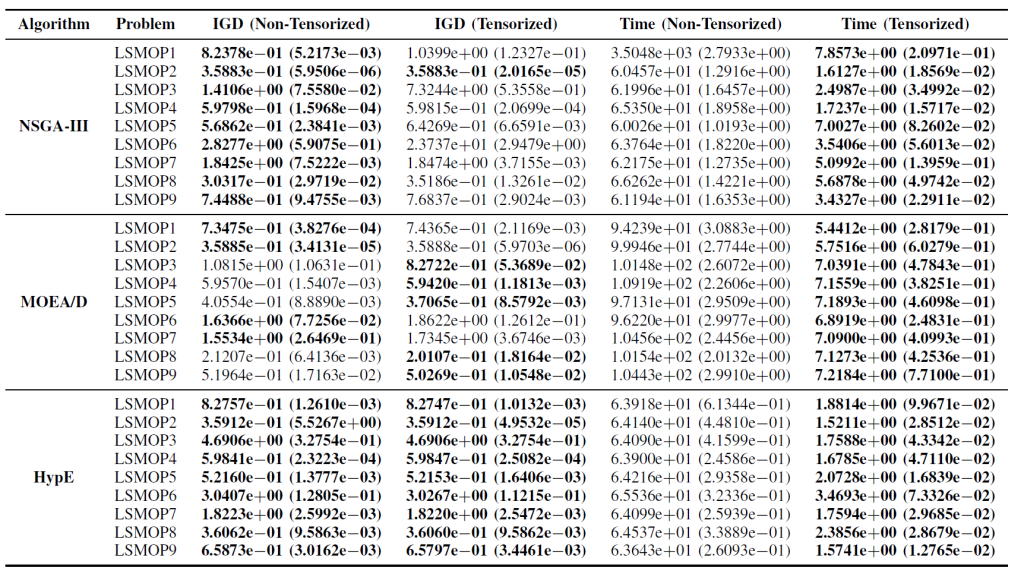
The findings indicate that GPU-accelerated, tensorized EMO algorithms substantially enhance computational efficiency while preserving or exceeding the optimization accuracy of their original counterparts.
Multiobjective Robot Control Tasks
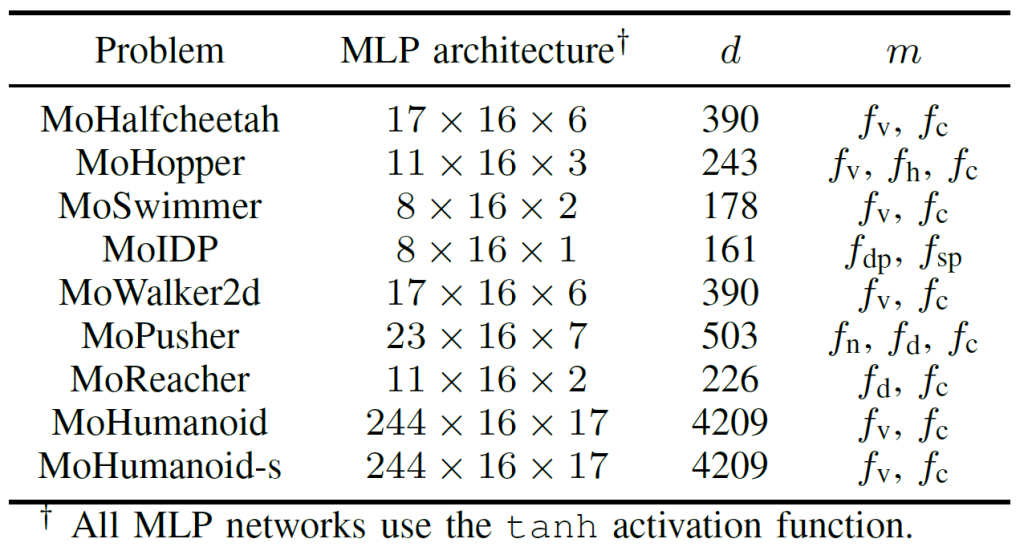
To assess real-world applicability, the EvoX team developed the MoRobtrol benchmark suite for multiobjective robot control, with tasks outlined in Table 3.
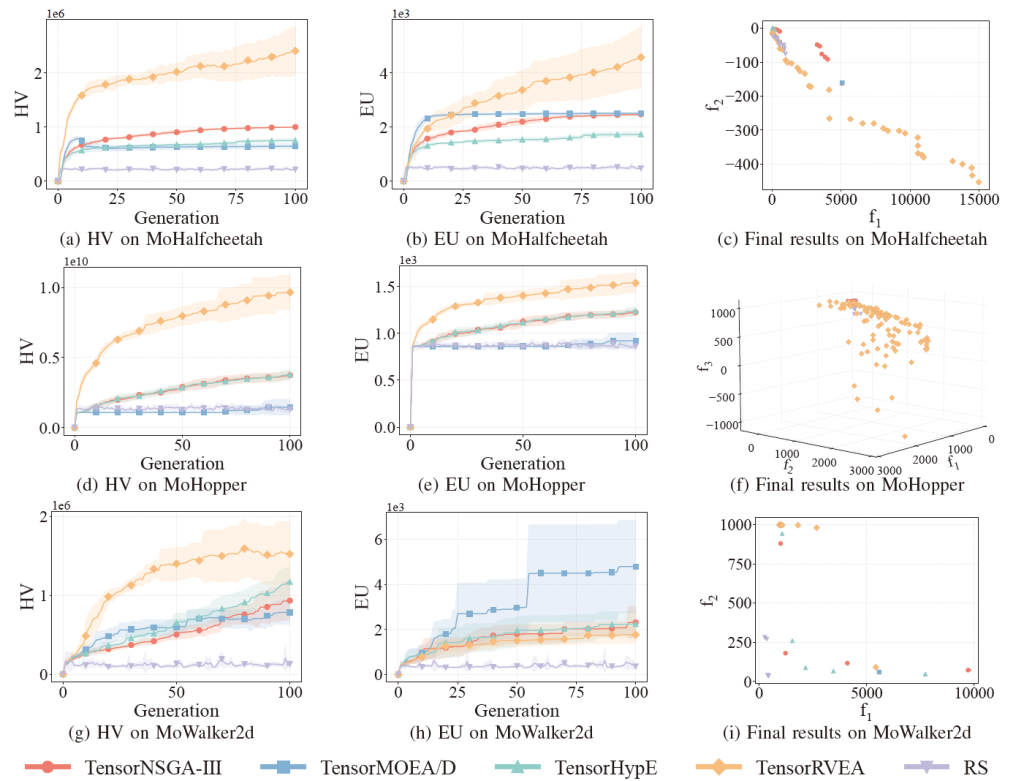
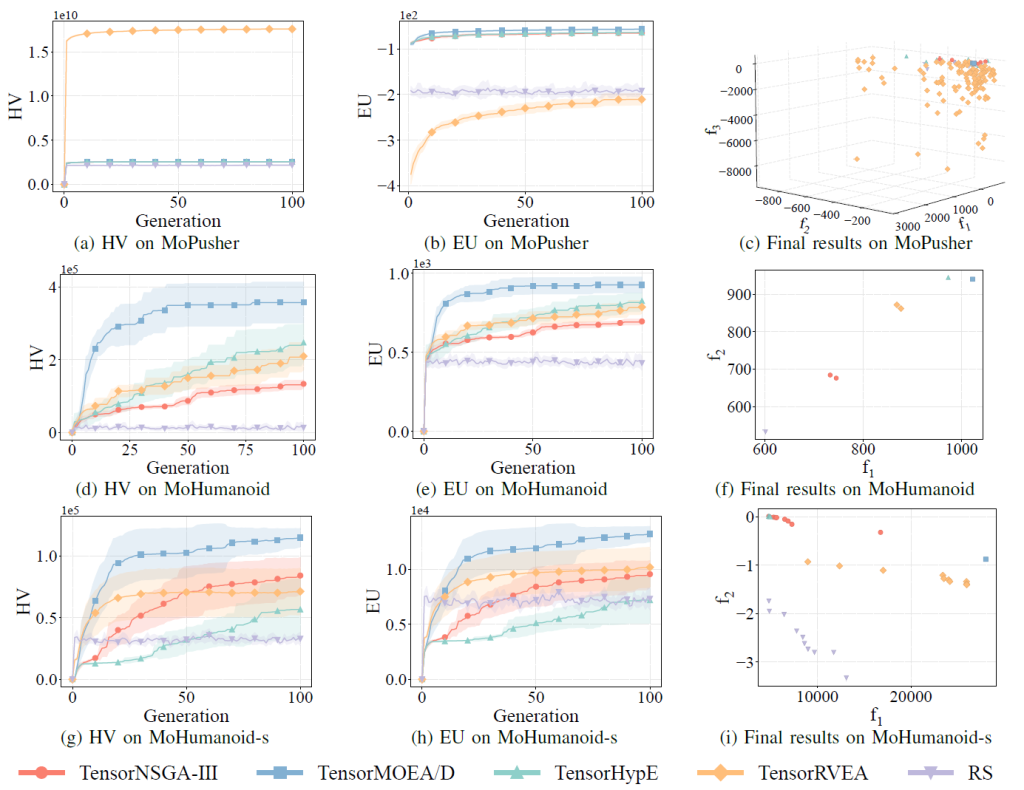
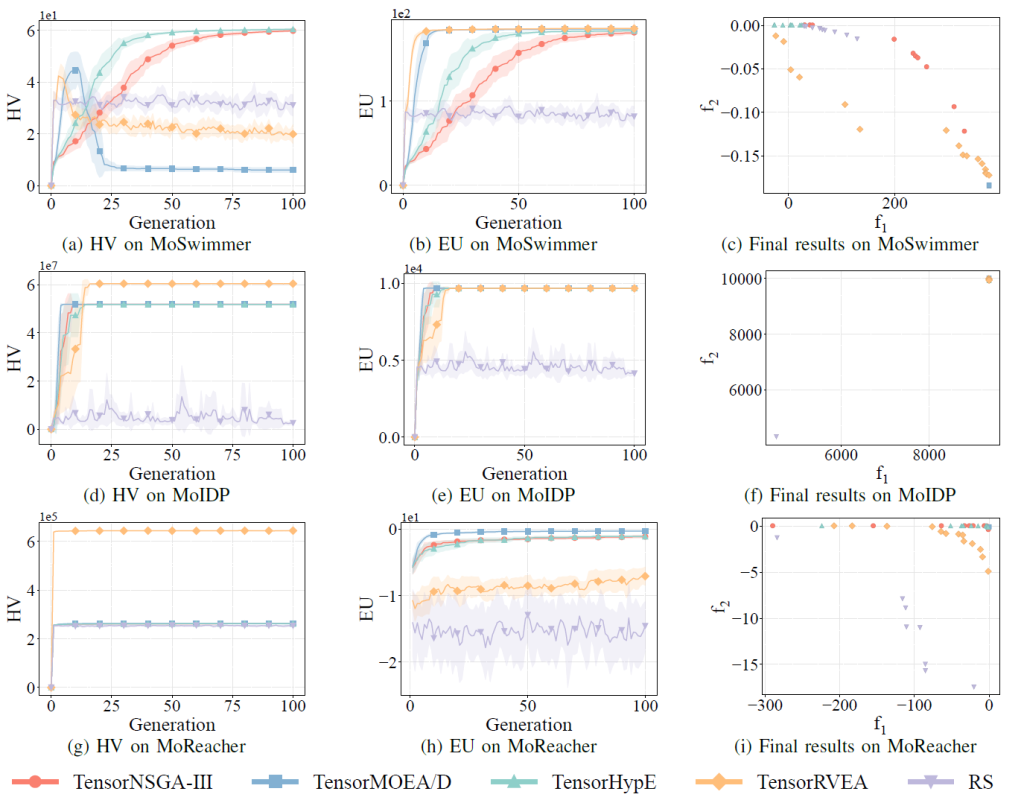
Performance comparisons of TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA, and Random Search (RS) across various MoRobtrol tasks—evaluated via Hypervolume (HV), Expected Utility (EU), and solution visualizations—are presented in Figures 6, 7, and 8. TensorRVEA emerges as the top performer, achieving the highest HV values and strong solution diversity across multiple environments. TensorMOEA/D excels in large-scale tasks, particularly in maintaining solution preference consistency. TensorNSGA-III and TensorHypE perform comparably, proving competitive in select scenarios. Overall, decomposition-based tensorized algorithms demonstrate a distinct advantage in addressing large-scale, complex problems.
Conclusion and Outlook
This study introduces a tensorized representation method to mitigate the computational efficiency and scalability limitations of traditional CPU-based EMO algorithms. Applied to representative algorithms such as NSGA-III, MOEA/D, and HypE, this approach yields substantial performance gains on GPUs without compromising solution quality. The development of the MoRobtrol benchmark suite further validates its practical utility, recasting robot control tasks in physical simulation environments as multiobjective optimization problems and highlighting the potential of tensorized algorithms in high-computational-demand fields like embodied intelligence. While tensorization markedly enhances efficiency, future research could explore several avenues for improvement, including optimizing core operators (e.g., non-dominated sorting), designing novel tensorized operations for multi-GPU configurations, and integrating large-scale data and deep learning techniques to further elevate algorithm performance in expansive optimization contexts.
Open source code / community
📄 Paper: https://arxiv.org/abs/2503.20286
🔗 GitHub: https://github.com/EMl-Group/evomo
🔼 Upstream Project (EvoX): https://github.com/EMI-Group/evox
🌐 QQ Communication Group: 297969717

EvoMO is constructed based on the EvoX framework. If you are interested in EvoX, please refer to the official blog articles of EvoX 1.0 for more details.