[IEEE TEVC] Accelerating Large-scale Multiobjective Optimization via Problem Reformulation

Cheng He et al.

Abstract:

---

With the progress in industrial automation, the demands for black-box multiobjective optimization with large-scale decision variables rise rapidly. Though evolutionary algorithms (EAs) are applicable to black-box optimization, their random search principle also leads to the unbearable cost of function evaluations. This work proposes to reformulate the large-scale multiobjective optimization problem into extremely low-dimensional ones, e.g., from 1000 to 20, aiming at obtaining acceptable solutions using 1/20 costs of conventional EAs. Moreover, this idea is also applicable to all existing EAs, enhancing their capability in solving large-scale multiobjective optimization problems with fewer function evaluations and computation time. Thanks to the low dimensionality of the weight variables and reduced objective space, a set of quasi-optimal solutions can be obtained efficiently. Finally, a multiobjective evolutionary algorithm is used to spread the quasi-optimal solutions over the approximate Pareto optimal front evenly. Experiments have been conducted on a variety of large-scale multiobjective problems with up to 5000 decision variables. Four different types of representative algorithms are embedded into the proposed framework and compared with their original versions, respectively. Furthermore, the proposed framework has been compared with two state-of-the-art algorithms for large-scale multiobjective optimization. The experimental results have demonstrated the significant improvement benefited from the framework in terms of its performance and computational efficiency in large-scale multiobjective optimization.

Paper  Code

Results

---

Performance on LSMOP Problems

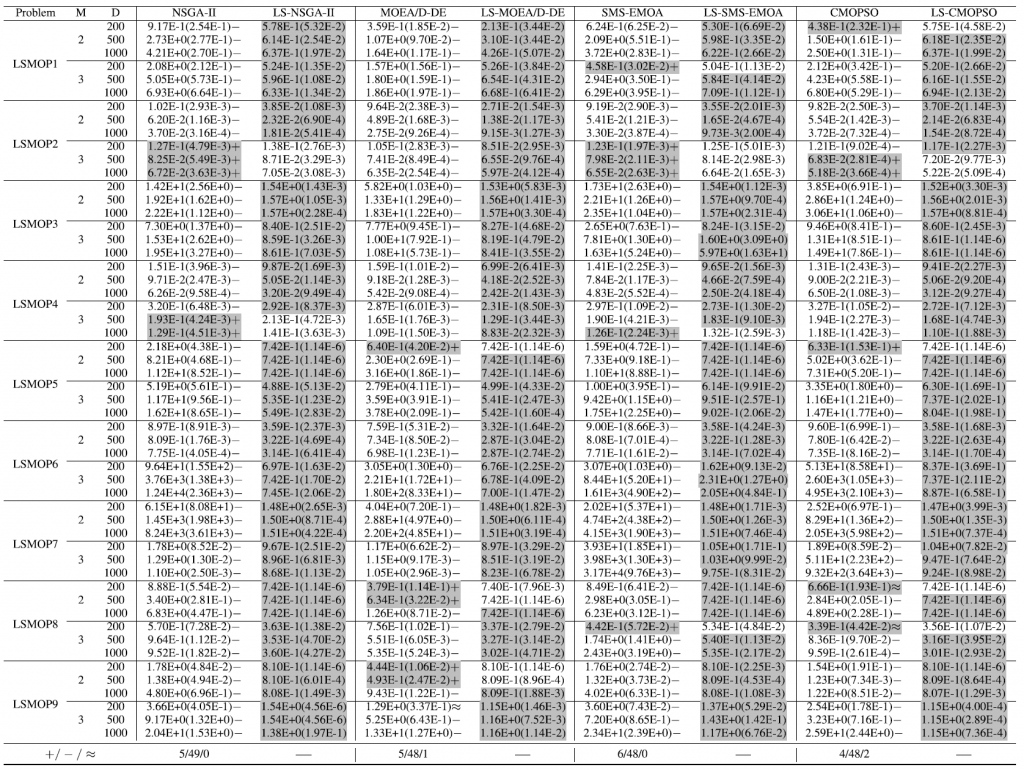
Table 1: Statics of IGD results obtained by eight compared algorithms on 54 test instances from LSMOP test suite. the best results in each two columns are highlighted.

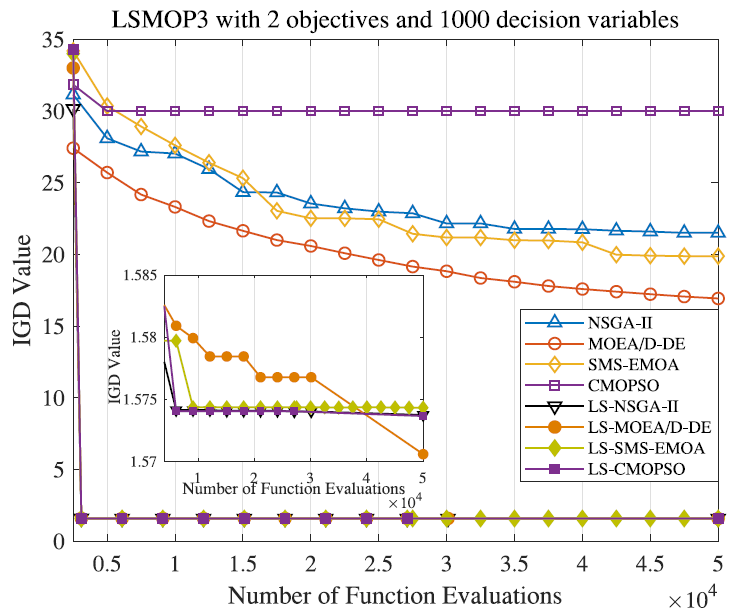
Figure 1: Convergence profiles of eight compared algorithms on bi-objective LSMOP3 and tri-objective LSMOP5 with 1000 decision variables.

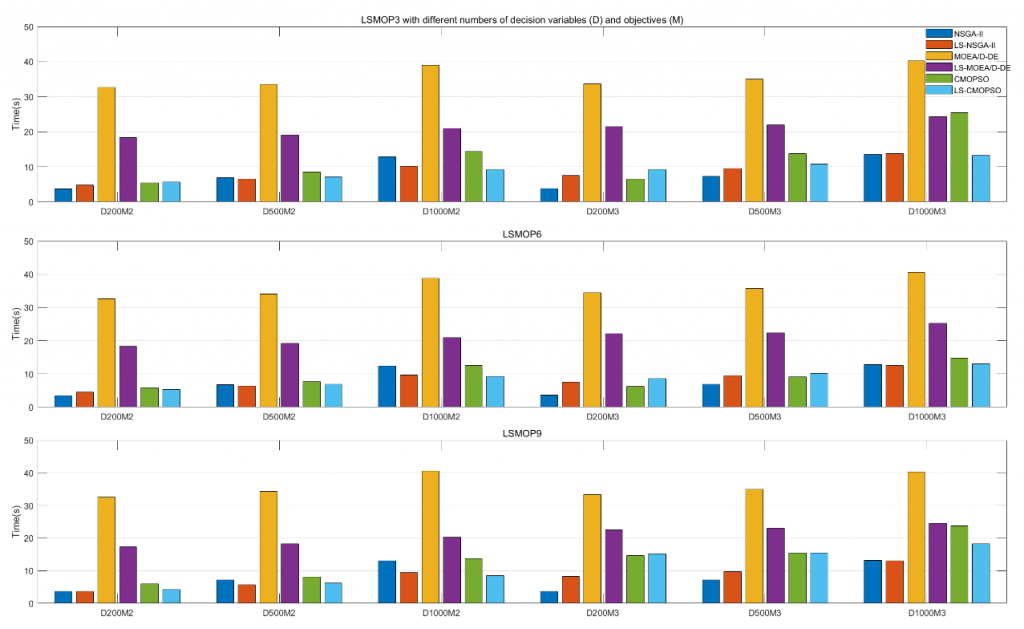
Figure 2: Average computation time of NSGA-II, MOEA/D-DE, CMOPSO, and their LSMOF-based versions on LSMOP3, LSMOP6, and LSMOP9, where M denotes the number of objectives and D denotes the number of decision variables.

Performance on DTLZ and WFG Problems

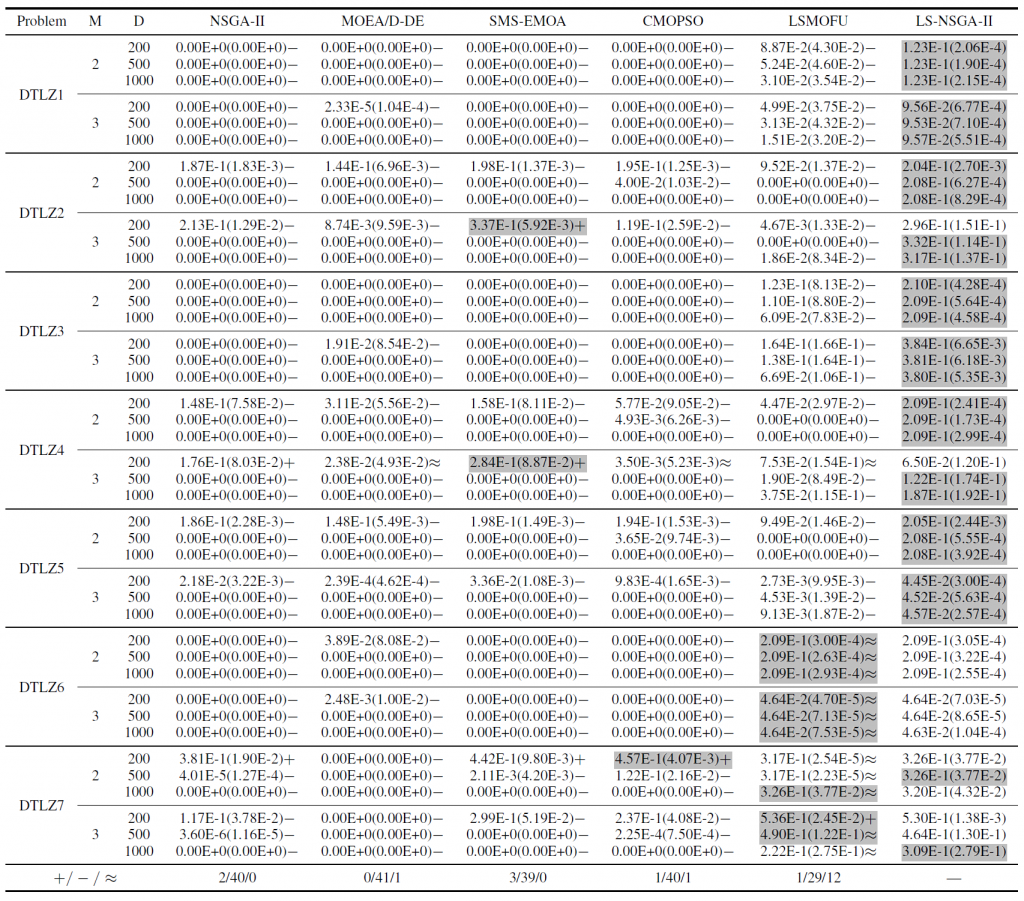
Table 3: The statics of HV results achieved by six compared algorithms on 54 test instances from WFG test suite. the best result in each row is highlighted.

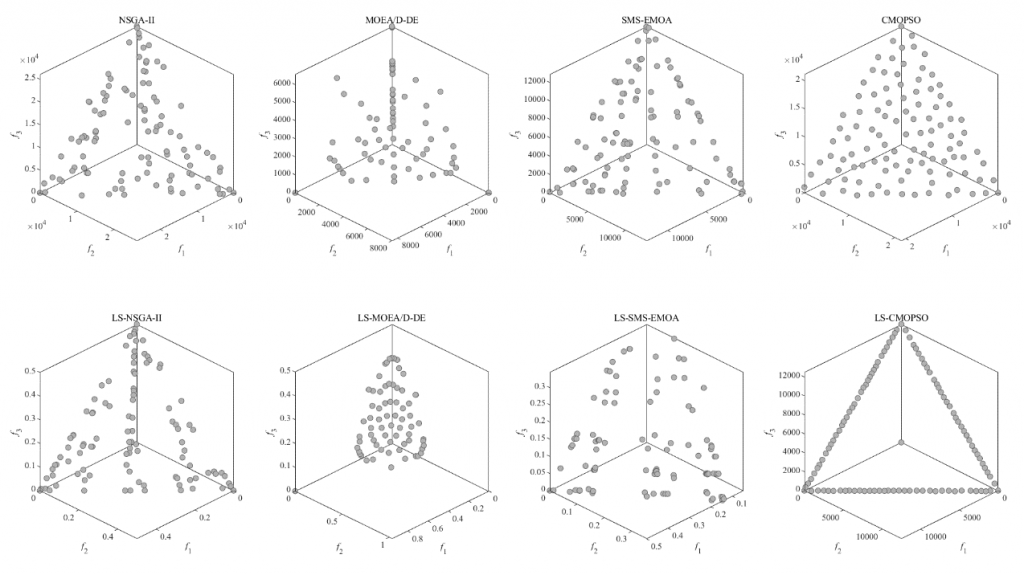
Figure 3: The final non-dominated Pareto front obtained by each algorithm on tri-objective DTLZ1 with 1000 decision variables in the run associated with the median IGD value.

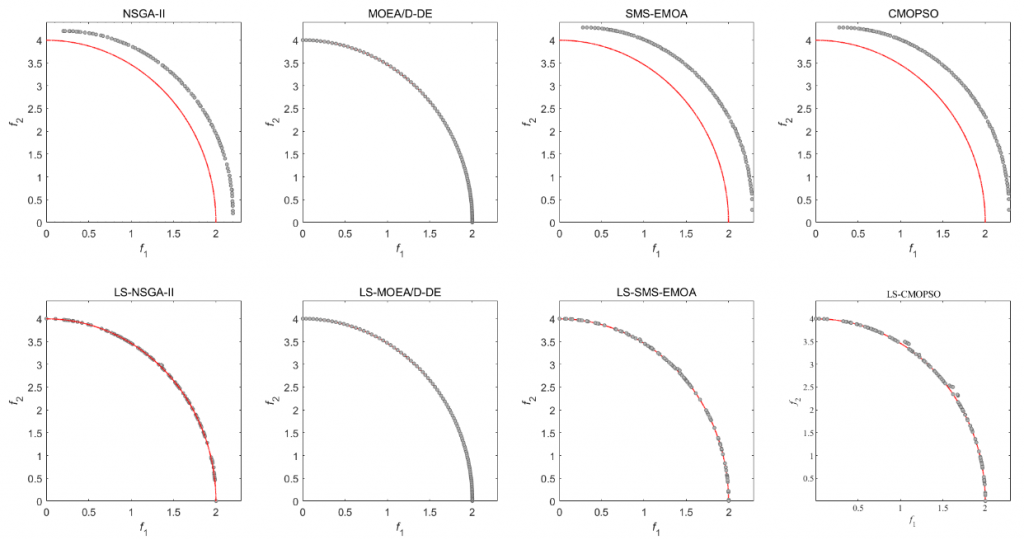
Figure 4: The final non-dominated Pareto front obtained by each algorithm on bi-objective WFG6 with 1000 decision variables in the run associated with the median IGD value. The red line is the PF of bi-objective WFG6.

Comparison with SOTA Large-scale MOEAs

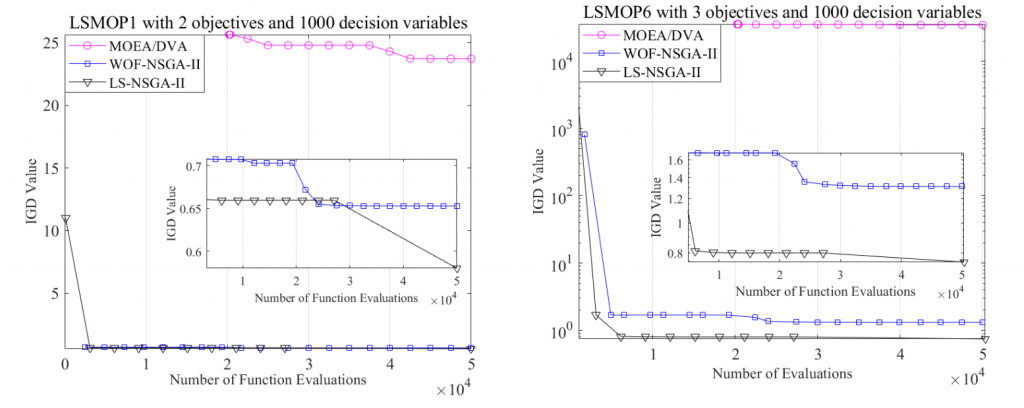
Figure 5: Convergence rates of three compared algorithms on bi-objective LSMOP1 and tri-objective LSMOP6 with 1000 decision variables.

Figure 6: Average computation time of MOEA/DVA, WOF-NSGA-II, and LS-NSGA-II on LSMOP1, where M is the number of objectives and D is the number of decision variables.

Bibtex

---

@article{he2019accelerating,
  title={Accelerating large-scale multiobjective optimization via problem reformulation},
  author={He, Cheng and Li, Lianghao and Tian, Ye and Zhang, Xingyi and Cheng, Ran and Jin, Yaochu and Yao, Xin},
  journal={IEEE Transactions on Evolutionary Computation},
  volume={23},
  number={6},
  pages={949--961},
  year={2019},
  publisher={IEEE}
}

Acknowledgments

---

This work was supported in part by the National Key Research and Development Program of China under Grant 2017YFC0804002, in part by the Program for Guangdong Introducing Innovative and Entrepreneurial Teams under Grant 2017ZT07X386, in part by the Shenzhen Peacock Plan under Grant KQTD2016112514355531, in part by the Science and Technology Innovation Committee Foundation of Shenzhen under Grant ZDSYS201703031748284, in part by the Program for University Key Laboratory of Guangdong Province under Grant 2017KSYS008, in part by the National Natural Science Foundation of China under Grant 61320106005 and Grant 61772214, and in part by Engineering and Physical Sciences Research Council under Grant EP/M017869/1.